3.4.7 Polynomial Division
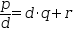
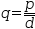
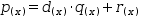
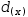
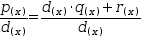
For example, polynomial division applied to
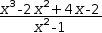

Polynomial division is useful in root finding. However, it is often just one step in a series of transformations.
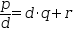
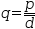
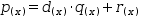
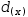
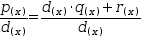
For example, polynomial division applied to
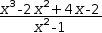

Polynomial division is useful in root finding. However, it is often just one step in a series of transformations.